The Capriccio Method
The Capriccio Method
The Capriccio method is a multiscale simulation approach particularly designed for multiscale simulations of amorphous polymers. It is a partitioned-domain concept which concurrently employs Molecular Dynamics (MD) and the Finite Element Method (FEM). The method, first published in [1], has been jointly developed by Sebastian Pfaller (Friedrich-Alexander-Universität Erlangen-Nürnberg/FAU – responsible for the coupling to the continuum) and by Mohammad Rahimi (then Technical University Darmstadt – responsible for the concept of stochastic boundary conditions).
Since then, extensive work has been done to investigate and to improve its performance [2,3] and it is continuously being enhanced for more complex systems like polymer nanocomposites [4] and for capturing fracture phenomena in polymers [5]. The Capriccio group promotes further developments as, e.g., enhanced treatment of surface effects in the MD domain [6], extension to inelasticity [7], and careful consideration of the equlibration procedure before load application [8]. The Capriccio method is vital part of the research grant of the German Research Foundation (DFG) on interphases in polymer nanocomposites, of the research training group GRK 2423 FRASCAL, and of the French-German project BIO ART addressing bio-based polymers.
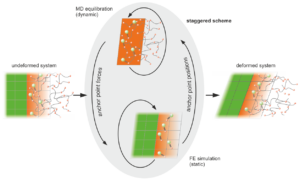
Figure 1: Staggered MD-FE scheme
The Capriccio algorithm is sketched in Fig. 1: Starting from the undeformed configuration, a load step is applied to the continuum and auxiliary particles, which are called anchor points, move according to the continuum displacement field. In this step, the particles in the MD domain are spatially fixed and exert forces on the moving anchor points due to harmonic interaction potentials. In the subsequent MD run, the anchor points form a fixed frame and confine the MD particles to their designated region. This concept of stochastic boundary conditions (SBC) is described in detail in [9] and enables, in contrast to convential periodic boundary conditions (PBC), an external, non-affine deformation of the MD part. Within a certain number of MD time steps, the system, which has been disturbed due to the change of anchor point positions, has to find a new equilibrium and provides updated MD particle positions to the subsequent continuum equilibration. This staggered scheme is carried out until the deformed system is obtained in equilibrium and another load step can be applied.
–PD Dr.-Ing. habil. Sebastian Pfaller (Akad. ORat)
Milestones
- Development of the Capriccio method
[1] S. Pfaller, M. Rahimi, G. Possart, P. Steinmann, F. Müller-Plathe, and M. C. Böhm, “An Arlequin-based method to couple molecular dynamics and finite element simulations of amorphous polymers and nanocomposites,” Computer Methods in Applied Mechanics and Engineering, vol. 260, pp. 109–129, 2013 http://dx.doi.org/10.1016/j.cma.2013.03.006
[2] S. Pfaller. “Multiscale Simulation of Polymers”. Dissertationsschrift, Friedrich-Alexander-Universität Erlangen-Nürnberg, 2015 https://nbn-resolving.org/urn:nbn:de:bvb:29-opus4-180624
[3] S. Pfaller. A. Kergaßner, and P. Steinmann, “Optimisation of the Capriccio method to couple particle– and continuum–based simulations of polymers,” Multiscale Science and Engineering, vol. 1, pp. 318-333, 2019 https://doi.org/10.1007/s42493-019-00028-y
[6] Y. Jain, M. Ries, S. Pfaller, and F. Müller-Plathe, “Addressing surface effects at the particle-continuum interface in a molecular dynamics and finite elements coupled multiscale simulation technique,” Journal of Chemical Theory and Computation, vol. 18, no. 4, pp. 2375-2387, 2022 https://doi.org/10.1021/acs.jctc.1c00940
[7] W. Zhao, P. Steinmann, and S. Pfaller, “A particle-continuum coupling method for multiscale simulations of viscoelastic-viscoplastic amorphous glassy polymers”, International Journal for Numerical Methods in Engineering, vol. 122, no. 24, pp. 7431-7451, 2021 https://doi.org/10.1002/nme.6836
[8] F. Weber, M. Ries, C. Bauer, C. R. Wick, and S. Pfaller, “On equilibrating non-periodic molecular dynamics samples for coupled particle-continuum simulations of amorphous polymers”, Forces in Mechanics, 10, 100159, 2023 https://doi.org/10.1016/j.finmec.2022.100159
[9] M. Rahimi, H. A. Karimi-Varzaneh, M. C. Böhm, F. Müller-Plathe, S. Pfaller, G. Possart, and P. Steinmann, “Nonperiodic stochastic boundary conditions for molecular dynamics simulations of materials embedded into a continuum mechanics domain,” Journal of Chemical Physics, vol. 134, p. 154108, 2011 https://doi.org/10.1063/1.3576122
- Application to polymer-particle interphases and polymer fracture
[4] M. Ries, F. Weber, G. Possart, P. Steinmann, and S. Pfaller, “A quantitative interphase model for polymer nanocomposites: Verification, validation, and consequences regarding size effects”, Composites Part A, available online, 107094, 2022 https://doi.org/10.1016/j.compositesa.2022.107094
[5] W. Zhao, Y. Jain, F. Müller-Plathe, P. Steinmann, and S. Pfaller, “Investigating fracture mechanisms in glassy polymers using coupled particle-continuum simulations”, Journal of the Mechanics and Physics of Solids, 193, 105884 https://doi.org/10.1016/j.jmps.2024.105884
